STA 506 2.0 Linear Regression Analysis
Interpretation of Regression Outputs
Dr Thiyanga S. Talagala
Recapping what we know
True linear regression model/ Population regression equation
μY|X=x=β0+β1x
how the mean of Y changes for given values of X.
We can also write the equation in terms of the observed values of Y, rather than the mean. Because the individual observations for any given value of X vary randomly about the mean of Y|X, we need to account for this random variation, or error, in the regression equation. Sample regression line
Yi=β0+β1xi+ϵi, i = 1, 2, 3...n
Please write the assumptions of ϵi
Fitted regression line
^Y=^β0+^β1x
Revisiting the fitted regression model
Fitted model
library(alr3) # to load the datasetLoading required package: carLoading required package: carDatamodel1 <- lm(Dheight ~ Mheight, data=heights)model1Call:lm(formula = Dheight ~ Mheight, data = heights)Coefficients:(Intercept) Mheight 29.9174 0.5417Model summary
summary(model1)Call:lm(formula = Dheight ~ Mheight, data = heights)Residuals: Min 1Q Median 3Q Max -7.397 -1.529 0.036 1.492 9.053 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 29.91744 1.62247 18.44 <2e-16 ***Mheight 0.54175 0.02596 20.87 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 2.266 on 1373 degrees of freedomMultiple R-squared: 0.2408, Adjusted R-squared: 0.2402 F-statistic: 435.5 on 1 and 1373 DF, p-value: < 2.2e-16R2 = 24.08%
Maybe you have one or more omitted variables. It is important to consider other factors that might influence the daughter's height:
Father's height
Physical activities performed by the daughter
Food nutrition, etc.
Maybe the functional form of the regression form is incorrect (so you have to add some quadratic, or cubic terms...). At the same time a transformation can be an alternative (if appropriate).
Maybe could be the effect of a group of outlier (maybe not one...).
A large R2 does not necessarily imply that the regression model will be an accurate predictor.
R2 does not measure the appropriateness of the linear model.
R2 will often large even though Y and X are nonlinearly related.
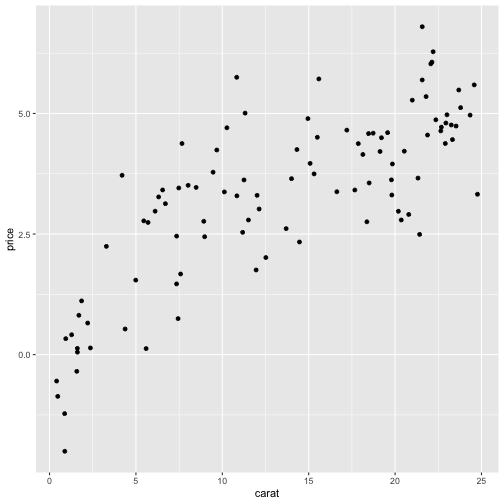
[1] 0.7834839Call:lm(formula = carat ~ price, data = df)Residuals: Min 1Q Median 3Q Max -2.91911 -0.66197 -0.07846 0.82734 2.97025 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.74996 0.23234 3.228 0.0017 ** price 0.18736 0.01501 12.481 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.137 on 98 degrees of freedomMultiple R-squared: 0.6138, Adjusted R-squared: 0.6099 F-statistic: 155.8 on 1 and 98 DF, p-value: < 2.2e-16- R2 is large even though the linear approximation is poor.
In general a good policy is to observe the scatterplot of your data

Y - Crystal size
X - Number of hours it takes crystal to grow
Data set
crystaldata <- data.frame(Size = c(0.08, 0.07, 1.12, 2.01, 4.43, 4.98, 4.92, 7.18, 5.57, 8.40, 8.81, 10.81, 11.61, 10.12, 13.12, 15.04, 0.075, 0.075, 1.13, 2.02, 4.45, 4.99, 4.95, 7.28, 5.67, 8.40, 8.51, 10.82, 11.62, 10.13, 13.22, 15.03), Time= c(2, 2, 4, 4,6, 8, 10, 12, 14, 16, 18, 20, 20, 24, 26, 28, 2, 2, 4, 4,6, 8, 10, 12, 14, 16, 18, 20, 20, 24, 26, 28))crystaldata Size Time1 0.080 22 0.070 23 1.120 44 2.010 45 4.430 66 4.980 87 4.920 108 7.180 129 5.570 1410 8.400 1611 8.810 1812 10.810 2013 11.610 2014 10.120 2415 13.120 2616 15.040 2817 0.075 218 0.075 219 1.130 420 2.020 421 4.450 622 4.990 823 4.950 1024 7.280 1225 5.670 1426 8.400 1627 8.510 1828 10.820 2029 11.620 2030 10.130 2431 13.220 2632 15.030 28scatterplot
ggplot(crystaldata, aes(x=Time, y = Size)) + geom_point()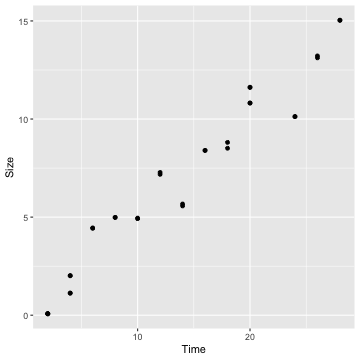
cor(crystaldata$Time, crystaldata$Size)[1] 0.9741803Fit a simple linear regression model
mod1 <- lm(Size ~ Time, data=crystaldata)mod1Call:lm(formula = Size ~ Time, data = crystaldata)Coefficients:(Intercept) Time -0.1982 0.5210Visualise the model
ggplot(crystaldata, aes(y=Size, x=Time))+geom_point(alpha=0.5) + geom_abline(intercept = -0.21, slope = 0.52, colour="forestgreen", lwd=2) + theme(aspect.ratio = 1)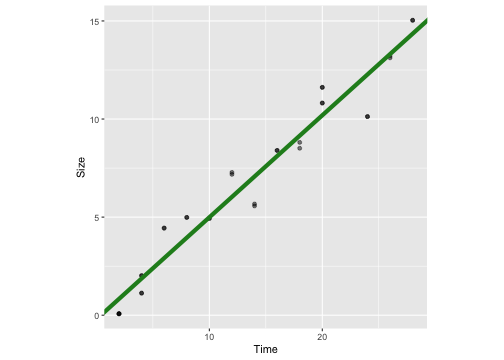
Questions
How well does this equation fit the data?
Are any of the basic assumptions violated?
summary(mod1)Call:lm(formula = Size ~ Time, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.1855 -0.7643 0.0313 0.7405 1.5223 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.19821 0.34838 -0.569 0.574 Time 0.52099 0.02204 23.634 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.05 on 30 degrees of freedomMultiple R-squared: 0.949, Adjusted R-squared: 0.9473 F-statistic: 558.5 on 1 and 30 DF, p-value: < 2.2e-16Coefficient of determination
Call:lm(formula = Size ~ Time, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.1855 -0.7643 0.0313 0.7405 1.5223 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.19821 0.34838 -0.569 0.574 Time 0.52099 0.02204 23.634 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.05 on 30 degrees of freedomMultiple R-squared: 0.949, Adjusted R-squared: 0.9473 F-statistic: 558.5 on 1 and 30 DF, p-value: < 2.2e-16- 94.5% of the variability in size is accounted by the regression model.
or
- 94.5% of the variation in size is explained by the number of hours it takes crystal to grow.
Are any of the basic assumptions violated?
mod1Call:lm(formula = Size ~ Time, data = crystaldata)Coefficients:(Intercept) Time -0.1982 0.5210Compute Residuals and Fitted values
library(broom)Warning: package 'broom' was built under R version 4.1.2mod1_fitresid <- augment(mod1)mod1_fitresid# A tibble: 32 × 8 Size Time .fitted .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 0.08 2 0.844 -0.764 0.0883 1.06 0.0281 -0.762 2 0.07 2 0.844 -0.774 0.0883 1.06 0.0289 -0.772 3 1.12 4 1.89 -0.766 0.0700 1.06 0.0215 -0.756 4 2.01 4 1.89 0.124 0.0700 1.07 0.000567 0.123 5 4.43 6 2.93 1.50 0.0552 1.03 0.0634 1.47 6 4.98 8 3.97 1.01 0.0440 1.05 0.0223 0.984 7 4.92 10 5.01 -0.0917 0.0363 1.07 0.000149 -0.0890 8 7.18 12 6.05 1.13 0.0321 1.05 0.0197 1.09 9 5.57 14 7.10 -1.53 0.0314 1.03 0.0354 -1.48 10 8.4 16 8.14 0.262 0.0343 1.07 0.00115 0.254 # … with 22 more rows1) The relationship between the response Y and the regressors is linear, at least approximately.
Plot of residuals vs fitted values and Plot of residuals vs predictor
Residuals vs Fitted
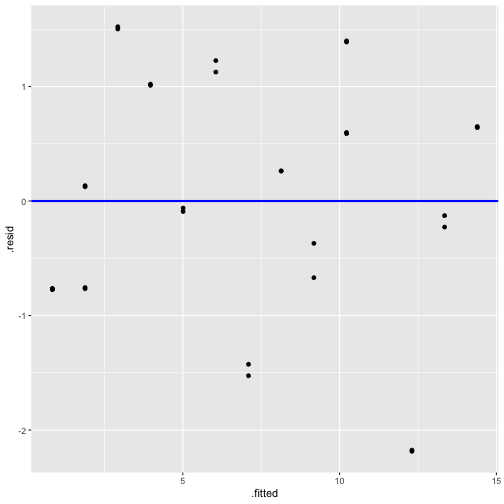
Residuals vs Time
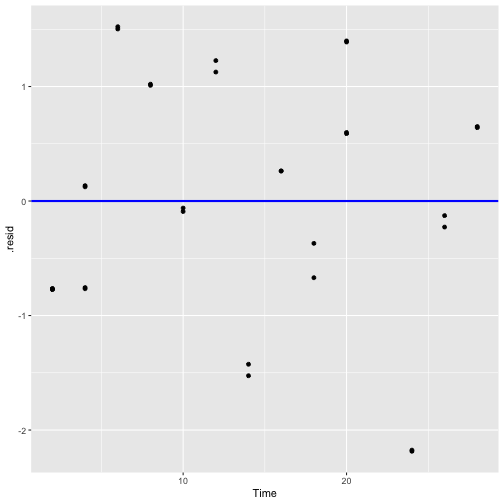
2) The error term ϵ has zero mean.
3) The error term ϵ has constant variance σ2.
Residuals vs Fitted
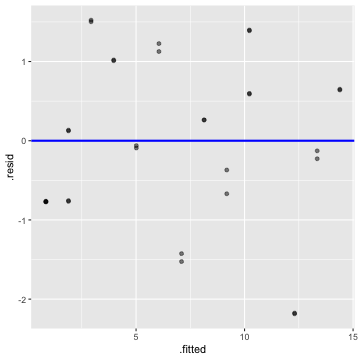
4) The error are uncorrelated.
5) The errors are normally distributed.
ggplot(mod1_fitresid, aes(x=.resid))+ geom_histogram(colour="white")+ggtitle("Distribution of Residuals")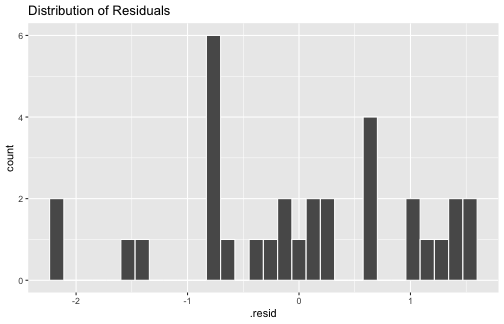
ggplot(mod1_fitresid, aes(sample=.resid))+ stat_qq() + stat_qq_line()+labs(x="Theoretical Quantiles", y="Sample Quantiles")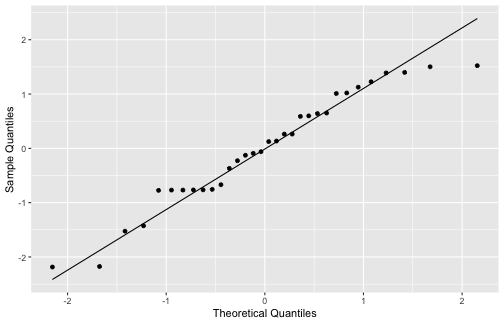
shapiro.test(mod1_fitresid$.resid) Shapiro-Wilk normality testdata: mod1_fitresid$.residW = 0.95397, p-value = 0.1867Interpretations
μY|X=x=β0+β1x
Slope:
Increase in the mean response for every one unit increase in the explanatory variable.
Intercept:
Mean response when the explanatory variable equals 0
mod1Call:lm(formula = Size ~ Time, data = crystaldata)Coefficients:(Intercept) Time -0.1982 0.5210Interpret slope and intercept
Nonsensical intercept interpretation
Sometimes it doesn't make sense to interpret the intercept: when?
X can never realistically take the value of zero, then the intercept is meaningless.
The intercept is negative even though the response can take only positive values.
The intercept helps the line fit the data as closely as possible.
It is fine to have a regression model with nonsensical intercept if it helps the model give better overall prediction accuracy.
Hypothesis testing on the slope and intercept
Hypothesis testing - Intercept
H0:β1=0
H1:β1≠0
summary(mod1)Call:lm(formula = Size ~ Time, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.1855 -0.7643 0.0313 0.7405 1.5223 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.19821 0.34838 -0.569 0.574 Time 0.52099 0.02204 23.634 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.05 on 30 degrees of freedomMultiple R-squared: 0.949, Adjusted R-squared: 0.9473 F-statistic: 558.5 on 1 and 30 DF, p-value: < 2.2e-16Situations where H0:β1=0 is not rejected.
In-class
Situations where H0:β1=0 is rejected.
In-class
Confidence Interval on β0 and β1
- Confidence intervals β0
[^β0−tα/2,n−2se(^β0),^β0+tα/2,n−2se(^β0)]
- Confidence intervals β1
[^β1−tα/2,n−2se(^β1),^β1+tα/2,n−2se(^β1)]
t-distribution
t0.025,30
qt(0.975, df=30)[1] 2.042272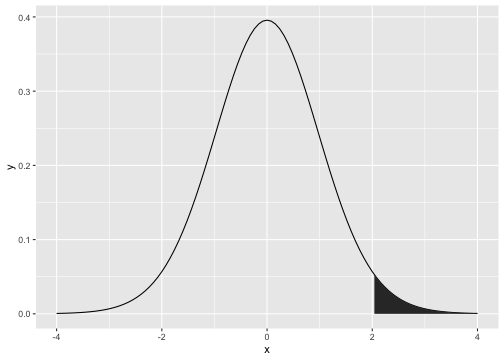
qt(0.025, df=30)[1] -2.042272summary(mod1)Call:lm(formula = Size ~ Time, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.1855 -0.7643 0.0313 0.7405 1.5223 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.19821 0.34838 -0.569 0.574 Time 0.52099 0.02204 23.634 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.05 on 30 degrees of freedomMultiple R-squared: 0.949, Adjusted R-squared: 0.9473 F-statistic: 558.5 on 1 and 30 DF, p-value: < 2.2e-16Compute confidence intervals on slope and intercept
Confidence Interval on β0 and β1 - Interpretation
- Confidence intervals β0
[^β0−tα/2,n−2se(^β0),^β0+tα/2,n−2se(^β0)]
- Confidence intervals β1
[^β1−tα/2,n−2se(^β1),^β1+tα/2,n−2se(^β1)]
Frequency interpretation:
If we were to take repeated samples of the same size at the same X levels and construct, for example, 95% confidence intervals on the slope for each sample, then 95% of those intervals will contain the true value β1.
We therefore have considerable confidence that the observed interval, here (04792, 0.5608), covers the true β1. The measure of confidence is .95. Here, .95 is called the confidence coefficient.
In general, the larger the confidence coefficient (1−α) is, the wider the confidence interval.
page 375, Mood and Graybill, Introduction to the theory of statistics
Analysis of variance - ANOVA
We may also use ANOVA to test the significance of regression.
The idea behind the ANOVA is that the variation in the response variable (referred to as the total variation - SST) is partitioned into two parts:
i. how much of the variation is explained by the regression model (referred to as the variable name in the R output) - SSM (Model sum of squares)
ii. how much of the variation is left unexplained by the regression model (called the “Residual” or “Error”) - SSE (Residual or error sum of squares).
n∑i=1(yi−¯y)2=n∑i=1(^Yi−¯y)2+n∑i=1(yi−^Yi)2
SST=SSM+SSE
Degrees of component
dfT=dfM+dfE n−1=1+(n−2)
ANOVA - F test
F=SSM/dfMSSE/dfE=MSMMSE
E(MSE)=σ2
ANOVA - Hypothesis
H0:β1=0 H1:β1≠0
In simple linear regression t-test is equivalent to the F test.
The real usefulness of the analysis of variance is in multiple regression models.
anova(mod1)Analysis of Variance TableResponse: Size Df Sum Sq Mean Sq F value Pr(>F) Time 1 615.46 615.46 558.55 < 2.2e-16 ***Residuals 30 33.06 1.10 ---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(mod1)Call:lm(formula = Size ~ Time, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.1855 -0.7643 0.0313 0.7405 1.5223 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.19821 0.34838 -0.569 0.574 Time 0.52099 0.02204 23.634 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.05 on 30 degrees of freedomMultiple R-squared: 0.949, Adjusted R-squared: 0.9473 F-statistic: 558.5 on 1 and 30 DF, p-value: < 2.2e-16Regression through the origin (No intercept)
Appropriate in analysing data from chemical and other manufacturing processes.
Do not misuse the no-intercept model: where the data lie in a region of x-space remote from the origin.
Scatterplot sometimes helps in deciding whether or not to fit the no-intercept model.
How to select the model: Fit both models (with intercept and without intercept) and choose between them based on the quality of the fit.
mod2 <- lm(Size ~ Time -1, data=crystaldata)mod2Call:lm(formula = Size ~ Time - 1, data = crystaldata)Coefficients: Time 0.5104summary(mod2)Call:lm(formula = Size ~ Time - 1, data = crystaldata)Residuals: Min 1Q Median 3Q Max -2.12895 -0.92631 -0.04059 0.78642 1.41254 Coefficients: Estimate Std. Error t value Pr(>|t|) Time 0.51037 0.01161 43.95 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 1.038 on 31 degrees of freedomMultiple R-squared: 0.9842, Adjusted R-squared: 0.9837 F-statistic: 1931 on 1 and 31 DF, p-value: < 2.2e-16With intercept
ggplot(crystaldata, aes(y=Size, x=Time))+geom_point(alpha=0.5) + geom_abline(intercept = -0.21, slope = 0.52, colour="forestgreen", lwd=2) + theme(aspect.ratio = 1)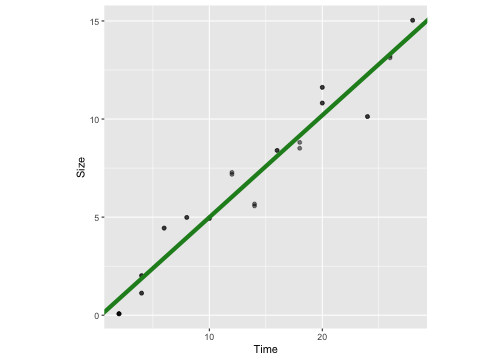
Without intercept
ggplot(crystaldata, aes(y=Size, x=Time))+geom_point(alpha=0.5) + geom_abline(intercept = 0, slope = 0.51, colour="red", lwd=2) + theme(aspect.ratio = 1)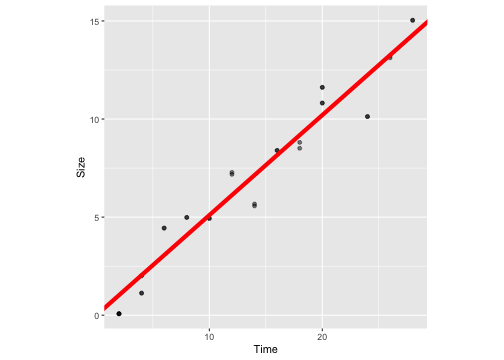
Perform the residual analysis on the new model before using it.
Prediction of new observations
test <- data.frame(Time = c(2, 2, 6, 6, 8, 20, 26))test Time1 22 23 64 65 86 207 26predict(mod2, newdata=test, interval="predict") fit lwr upr1 1.020746 -1.0972070 3.1386992 1.020746 -1.0972070 3.1386993 3.062237 0.9400507 5.1844244 3.062237 0.9400507 5.1844245 4.082983 1.9570988 6.2088676 10.207457 8.0376929 12.3772227 13.269695 11.0645387 15.474851Next Lecture
Multiple linear regression
Acknowledgement
Introduction to Linear Regression Analysis, Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining
All rights reserved by