STA 506 2.0 Linear Regression Analysis

STA 506 2.0 Linear Regression AnalysisLecture 12-i: Identifying Outliers and Influential CasesDr Thiyanga S. Talagala1 / 26

What exactly is an outlier?

No hard and fast definition.
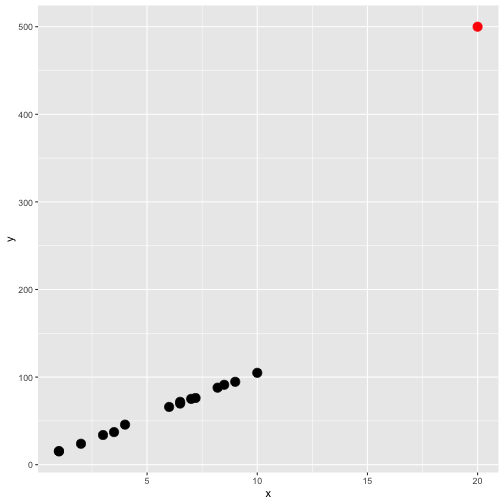
An outlier is a data point which is very far, somehow, from the rest of the data.

Would you consider the red point in either plot as outliers?

2 / 26

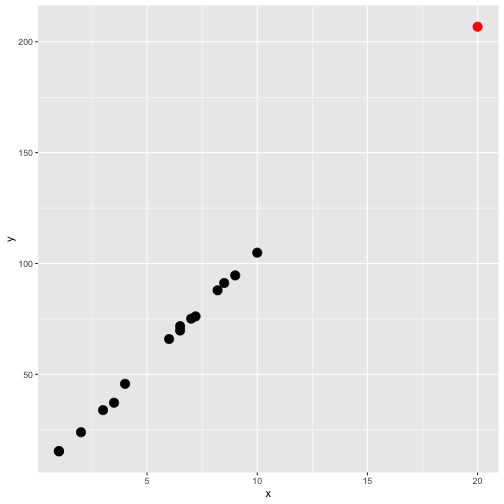
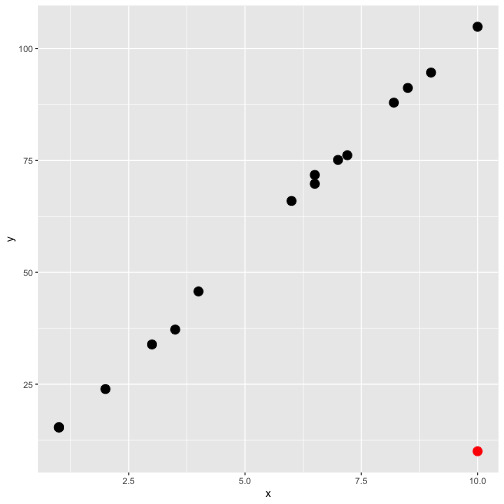
Outliers should be carefully studied for

why they occurred and
whether they should be retained in the model.

3 / 26

Types of outliers that occur in the context of regression

regression outlier
residual outlier
x-space outlier
y-space outlier
x- and y-space outlier

4 / 26

1. Regression outlier

lies off the line fit to the other 15 observations
determined from the remaining $(n - 1)$ observations.

5 / 26

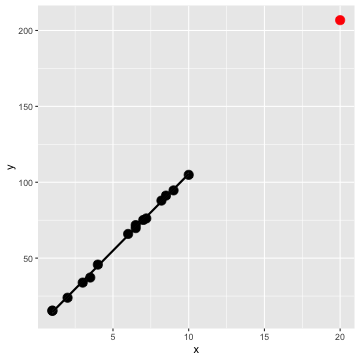
2. Residual outlier

A point that has large standardized or studentized residual when it is used with all $n$ observations to fit a model.

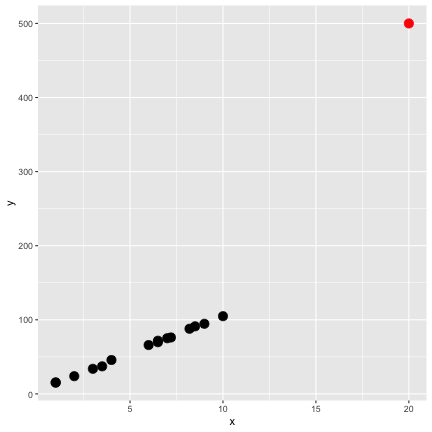
           y    x
1   15.37697  1.0
2   15.30155  1.0
3   23.90198  2.0
4   33.86959  3.0
5   37.20347  3.5
6   45.72057  4.0
7   65.93912  6.0
8   69.77062  6.5
9   71.75913  6.5
10  75.11737  7.0
11  76.14688  7.2
12  87.90926  8.2
13  91.19637  8.5
14  94.62842  9.0
15 104.87674 10.0
16 500.00000 20.0

6 / 26

2. Residual outlier (cont.)

lmfit <- lm(y~x, data=example.data)
library(broom)
augment(lmfit)

# A tibble: 16 × 8
       y     x .fitted .resid   .hat .sigma  .cooksd .std.resid
   <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
 1  15.4   1    -35.7    51.0 0.157   46.3   0.130        1.18 
 2  15.3   1    -35.7    51.0 0.157   46.3   0.129        1.18 
 3  23.9   2    -13.0    36.9 0.125   47.5   0.0505       0.840
 4  33.9   3      9.63   24.2 0.100   48.3   0.0165       0.543
 5  37.2   3.5   21.0    16.2 0.0902  48.6   0.00651      0.362
 6  45.7   4     32.3    13.4 0.0816  48.6   0.00396      0.298
 7  65.9   6     77.6   -11.6 0.0632  48.7   0.00220     -0.256
 8  69.8   6.5   88.9   -19.1 0.0625  48.5   0.00588     -0.420
 9  71.8   6.5   88.9   -17.1 0.0625  48.5   0.00472     -0.376
10  75.1   7    100.    -25.1 0.0634  48.3   0.0103      -0.552
11  76.1   7.2  105.    -28.6 0.0642  48.1   0.0136      -0.629
12  87.9   8.2  127.    -39.5 0.0720  47.4   0.0295      -0.872
13  91.2   8.5  134.    -43.0 0.0756  47.2   0.0370      -0.951
14  94.6   9    146.    -50.9 0.0828  46.5   0.0577      -1.13 
15 105.   10    168.    -63.3 0.102   45.1   0.115       -1.42 
16 500    20    395.    105.  0.641    1.14 12.5          3.74

7 / 26

2. Residual outlier (cont.)

Distribution of .std.resid in the previous output.

8 / 26

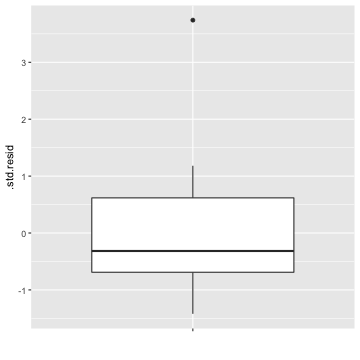
3. X-space outlier

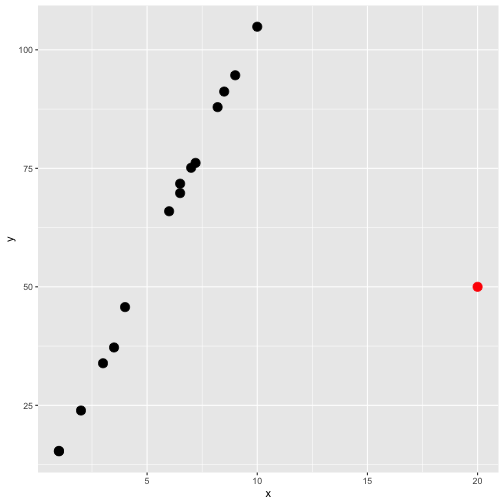
Hight leverage point

A data point can be unusual in its x variables.

9 / 26

4. Y-space outlier

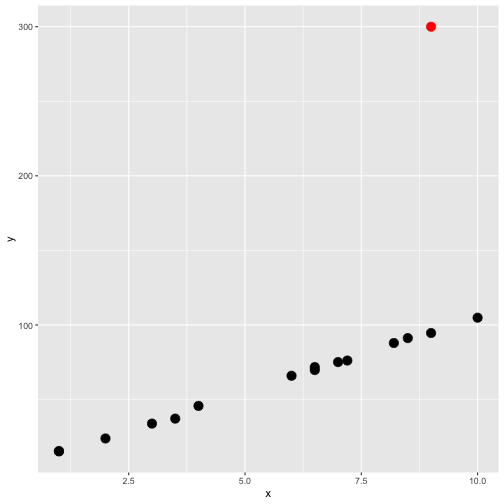
High discrepancy point

A point has an unusual y-value given its x-value.

10 / 26

5. X- and Y-space outlier

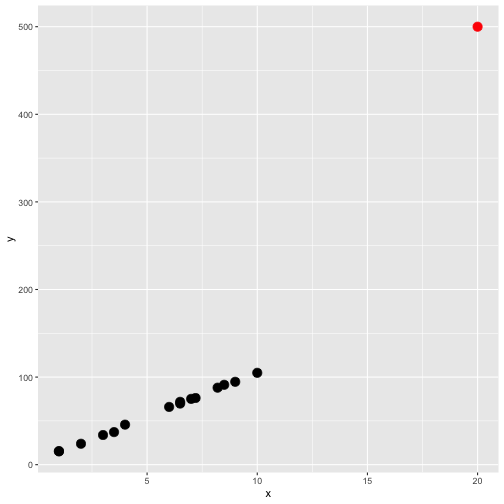
point that has both high leverage and high discrepancy

11 / 26

Least-squares regression fit

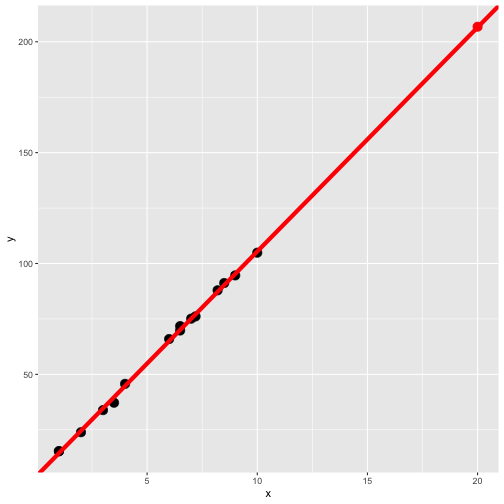
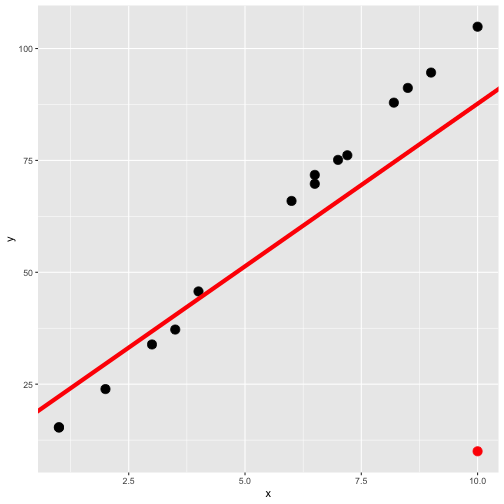
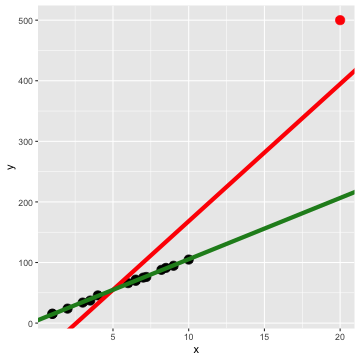
Red line: all data including the red point.

12 / 26

Least-squares regression fit

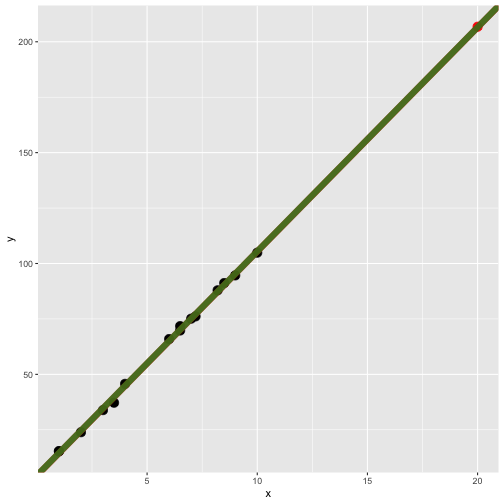
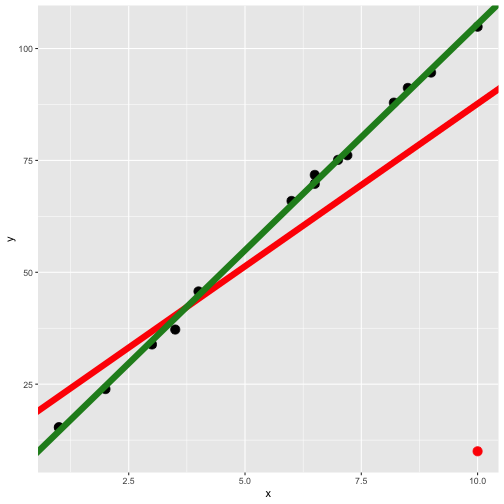
Red line: all data including the red point.

Green line: for all black point (without red point).

13 / 26

Assessing leverage

Hat (leverages) value: Helps to identify extreme $X$ values.

In simple linear regression

$h_{i i} = \frac{1}{n} + \frac{(x_{i} - \bar{x})^{2}}{\sum_{j = 1}^{n} (x_{j} - \bar{x})^{2}},$

where $i = 1, 2, . . . n$

Hat value is bound between $1 / n$ and 1, with 1 denoting highest leverage.

n - total number of points

14 / 26

Assessing leverage (cont.)

In multiple linear regression

$Y = β_{0} + β_{1} X_{1} + β_{2} X_{2} + . . . + β_{p} X_{p} + ϵ$

$Y = [\begin{matrix} Y_{1} \\ Y_{2} \\ . \\ . \\ . \\ Y_{n} \end{matrix}]$

$X = [\begin{matrix} 1 x_{11} x_{12} . . . x_{1 p} \\ 1 x_{21} x_{22} . . . x_{2 p} \\ . \\ . \\ . \\ 1 x_{n 1} x_{n 2} . . . x_{n p} \end{matrix}]$

$H = X (X^{'} X)^{- 1} X^{'}$

Hat matrix diagonal is a standardized measure of the distance of the $i$ th observation from the center (or centroid) of the $x -$ space.

The leverage (hat) value $h_{i i}$ does not depend on the response $Y_{i}$ .

15 / 26

Assessing leverage: Example

           y    x
1   15.37697  1.0
2   15.30155  1.0
3   23.90198  2.0
4   33.86959  3.0
5   37.20347  3.5
6   45.72057  4.0
7   65.93912  6.0
8   69.77062  6.5
9   71.75913  6.5
10  75.11737  7.0
11  76.14688  7.2
12  87.90926  8.2
13  91.19637  8.5
14  94.62842  9.0
15 104.87674 10.0
16 500.00000 20.0

16 / 26

Assessing leverage: Example (cont)

library(broom)
data.fit <- lm(y ~x, data=example.data)
augment(data.fit)

# A tibble: 16 × 8
       y     x .fitted .resid   .hat .sigma  .cooksd .std.resid
   <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
 1  15.4   1    -35.7    51.0 0.157   46.3   0.130        1.18 
 2  15.3   1    -35.7    51.0 0.157   46.3   0.129        1.18 
 3  23.9   2    -13.0    36.9 0.125   47.5   0.0505       0.840
 4  33.9   3      9.63   24.2 0.100   48.3   0.0165       0.543
 5  37.2   3.5   21.0    16.2 0.0902  48.6   0.00651      0.362
 6  45.7   4     32.3    13.4 0.0816  48.6   0.00396      0.298
 7  65.9   6     77.6   -11.6 0.0632  48.7   0.00220     -0.256
 8  69.8   6.5   88.9   -19.1 0.0625  48.5   0.00588     -0.420
 9  71.8   6.5   88.9   -17.1 0.0625  48.5   0.00472     -0.376
10  75.1   7    100.    -25.1 0.0634  48.3   0.0103      -0.552
11  76.1   7.2  105.    -28.6 0.0642  48.1   0.0136      -0.629
12  87.9   8.2  127.    -39.5 0.0720  47.4   0.0295      -0.872
13  91.2   8.5  134.    -43.0 0.0756  47.2   0.0370      -0.951
14  94.6   9    146.    -50.9 0.0828  46.5   0.0577      -1.13 
15 105.   10    168.    -63.3 0.102   45.1   0.115       -1.42 
16 500    20    395.    105.  0.641    1.14 12.5          3.74

17 / 26

Assessing leverage: Example (cont)

$cut off = \frac{2 p}{n},$

$p$ - number of predictors/ x- variables.

$n$ - number of observations.

In this case $cut off = \frac{2 p}{n} = \frac{2 \times 1}{16} = 0.125$

We say a point is a high leverage point if

$h_{i i} > \frac{2 p}{n}$

This cut off does not apply $\frac{2 p}{n} > 1$ .

18 / 26

What to do when you find outliers?Explore! (data entry errors, recording errors, etc.)
19 / 26

Influence

a point with high leverage can dramatically impact the regression model.

All points (red)

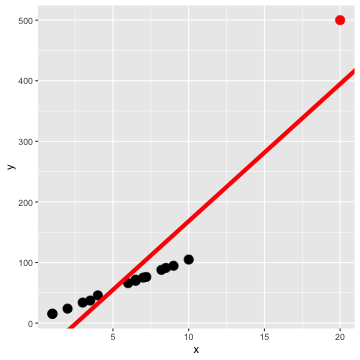
Only black points (green)

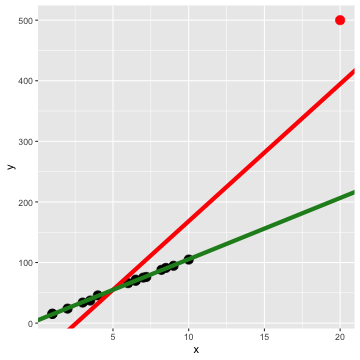
Influence - measures how much impact a point has on the regression model

20 / 26

Measure of Influence (cont.)

Cook's distance, $D_{i}$ , is a measure of influence.

augment(data.fit)

# A tibble: 16 × 8
       y     x .fitted .resid   .hat .sigma  .cooksd .std.resid
   <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
 1  15.4   1    -35.7    51.0 0.157   46.3   0.130        1.18 
 2  15.3   1    -35.7    51.0 0.157   46.3   0.129        1.18 
 3  23.9   2    -13.0    36.9 0.125   47.5   0.0505       0.840
 4  33.9   3      9.63   24.2 0.100   48.3   0.0165       0.543
 5  37.2   3.5   21.0    16.2 0.0902  48.6   0.00651      0.362
 6  45.7   4     32.3    13.4 0.0816  48.6   0.00396      0.298
 7  65.9   6     77.6   -11.6 0.0632  48.7   0.00220     -0.256
 8  69.8   6.5   88.9   -19.1 0.0625  48.5   0.00588     -0.420
 9  71.8   6.5   88.9   -17.1 0.0625  48.5   0.00472     -0.376
10  75.1   7    100.    -25.1 0.0634  48.3   0.0103      -0.552
11  76.1   7.2  105.    -28.6 0.0642  48.1   0.0136      -0.629
12  87.9   8.2  127.    -39.5 0.0720  47.4   0.0295      -0.872
13  91.2   8.5  134.    -43.0 0.0756  47.2   0.0370      -0.951
14  94.6   9    146.    -50.9 0.0828  46.5   0.0577      -1.13 
15 105.   10    168.    -63.3 0.102   45.1   0.115       -1.42 
16 500    20    395.    105.  0.641    1.14 12.5          3.74

21 / 26

Measure of Influence (cont.)

We usually consider points for which $D_{i} > 1$ to be influential (Montgomery, et al.).

# A tibble: 16 × 8
       y     x .fitted .resid   .hat .sigma  .cooksd .std.resid
   <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
 1  15.4   1    -35.7    51.0 0.157   46.3   0.130        1.18 
 2  15.3   1    -35.7    51.0 0.157   46.3   0.129        1.18 
 3  23.9   2    -13.0    36.9 0.125   47.5   0.0505       0.840
 4  33.9   3      9.63   24.2 0.100   48.3   0.0165       0.543
 5  37.2   3.5   21.0    16.2 0.0902  48.6   0.00651      0.362
 6  45.7   4     32.3    13.4 0.0816  48.6   0.00396      0.298
 7  65.9   6     77.6   -11.6 0.0632  48.7   0.00220     -0.256
 8  69.8   6.5   88.9   -19.1 0.0625  48.5   0.00588     -0.420
 9  71.8   6.5   88.9   -17.1 0.0625  48.5   0.00472     -0.376
10  75.1   7    100.    -25.1 0.0634  48.3   0.0103      -0.552
11  76.1   7.2  105.    -28.6 0.0642  48.1   0.0136      -0.629
12  87.9   8.2  127.    -39.5 0.0720  47.4   0.0295      -0.872
13  91.2   8.5  134.    -43.0 0.0756  47.2   0.0370      -0.951
14  94.6   9    146.    -50.9 0.0828  46.5   0.0577      -1.13 
15 105.   10    168.    -63.3 0.102   45.1   0.115       -1.42 
16 500    20    395.    105.  0.641    1.14 12.5          3.74

22 / 26

Leverage and Influence

Remember that leverage alone does not mean a point exerts high influence, but it certainly means it's worth investigating.

23 / 26

Influence

An influence point, can make a noticeable impact on the model coefficients in that it pulls the regression model in its direction.

All points

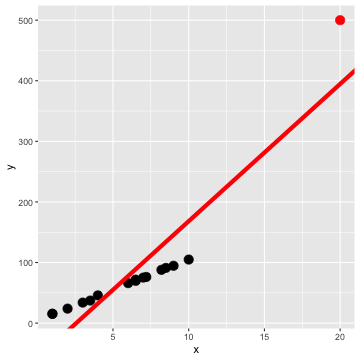
Only black points (green)

24 / 26

Other Measures of Influence

DEFITS and DFBEATAS

Treatment of Influential Observations

Should influential points ever be discarded? If there is a recording error, measurement error, or if the sample point is invalid or not part of the population that was intended to be sampled, then deleting the point is appropriate.
The field of robust statistics is concerned with more advanced methods of dealing with influential outliers. For e.g.: down weight observations in proportional to residual magnitude or influence. Then highly influential observations will receive less weight than they would in a least-squares fit. e.g: Robust regression

25 / 26

Acknowledgement

Introduction to Linear Regression Analysis, Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining

Dr. Thiyanga S. Talagala

26 / 26

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help